 Partial Products is a nice little method for multiplying large numbers. I recommend showing students how to do this method of multiplying before introducing them to the traditional algorithm - the way I learned to do it in school, which was the only method we were ever taught. To multiply 2-digit numbers, have kids begin by splitting up the numbers into expanded notation - hundreds, tens and ones. For example, to do 38 x 7, think of 38 as 30 and 8. Now multiply those numbers by 7. So, 30 x 7 = 210 and 8 x 7 = 56. 210 + 56 = 266, therefore 38 x 7 = 266. The picture above shows this thinking symbolically. 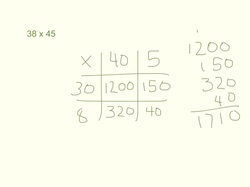 Use this method for larger numbers as well. 38 x 45 is 30 x 40, 30 x 5, 40 x 8 and 5 x 8. The picture at the left explains this thinking a bit more clearly. Once you have all the multiplication finished, just add the products together to get the final product of 38 x 45. To those of us who are used to multiplying with regrouping (carrying the tens, hundreds, etc) this sounds complicated, but kids will get the partial products method way faster than the traditional method. Once they understand how to multiply larger numbers, then definitely introduce the shortcut, which is the traditional algorithm, but don't introduce it too soon! If kids learn to do the steps of the traditional method before they understand why those steps work, we are setting them up for a lifetime of math phobia. Check out my YouTube video below for a full explanation of this method, as well as the Partial Quotients method of dividing large numbers, which I explain below. 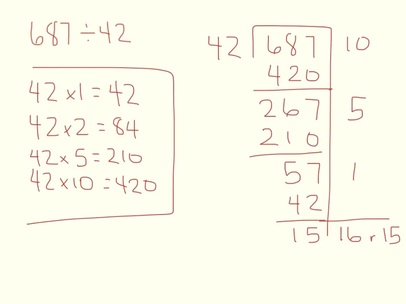 OK, now let's use this method of partial "answers" and apply it to division as an alternative to long division, which is a much hated concept across middle years students (at least, I hated it!). To begin the Partial Quotients method of division, I like to start with a quick list of multiplication facts, which will lessen the mental load I'm carrying while I do the division. So if I'm dividing by 3, I make a list of the 3x facts that can help me - specifically, 3x1, 3x2, 3x5 and 3x10. The example in the picture above shows the facts of 42 that I can draw on to solve 687÷42. Next I think about how many groups of 42 I can take from 687. I use the facts I recorded to check. I see that I can take 10 groups away, so I record that, and take the 10 groups away. Now I still have 267, so I can take 5 groups of 42 away from that, which is 210. I still have 57, so I take one more group of 42 away and I have 15 left over. That means I have taken away 16 groups of 42 and there is a remainder of 15. Therefor, 687÷42=16 r15. Easy peasy. As I mentioned with the multiplication strategy above, introduce this method before you show students the traditional method of "long division." If you introduce the standard algorithm too early, there is the danger of kids learning the "dance steps" without understanding the concept. This is setting them up for failure down the road. I encourage you to watch the video, as the method is easier to understand when you see it in action. Good luck!
0 Comments
Leave a Reply. |
Details
Lori EmilsonTravelling Curriculum Support Teacher Archives
April 2017
Categories
All
|
 RSS Feed
RSS Feed
